Ejercicios resueltos. Descomposición de un número en factores primos. Método rápido. Árbol de factores

Factores primos

El factor es un número que puede dividir a otro sin residuo, es decir, exactamente.
Ejemplo: Los factores de 16 son 1, 2, 4, 8 y 16 porque:

Un factor es primo cuando sólo puede dividirse por sí mismo y por la unidad. Ejemplo:

Para obtener los factores primos de un número se pueden utilizar dos métodos: la descomposición por divisiones sucesivas en tabla y la descomposición a través del árbol de factores.
El método de la descomposición por divisiones sucesivas en tabla lo explico en el tema: Descomposición de un número en factores primos de este sitio.
Aquí voy a explicar el método del árbol de factores, que es un diagrama en el que se muestran los factores primos de un número.
Es un método rápido pero debes cumplir con los siguientes requisitos:
a) En las ramas del árbol nunca puedes escribir el 1.
b) Si al querer elaborar el árbol de factores de un número sólo tienes como factores al 1 y al mismo número, entonces el número original es un número primo y no se puede hacer el árbol de factores.
Ejemplo: El 13 sólo puede dividirse entre 1 y entre sí mismo, por ello no puede realizarse el árbol de factores.
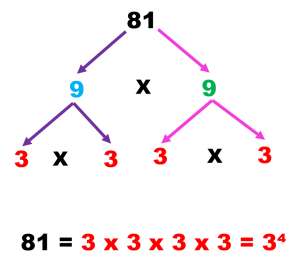
c) Cuando escribes números primos en un árbol, éstos ya no se factorizan.
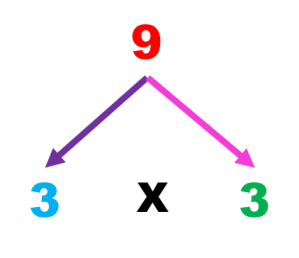
Ejemplo: El árbol de factores del 9 es 3 x 3 y como el 3 es factor primo, así se queda

d) El resultado se queda representado como árbol o puedes indicarlo como una multiplicación de factores.

Veamos ejemplos con diferentes números.

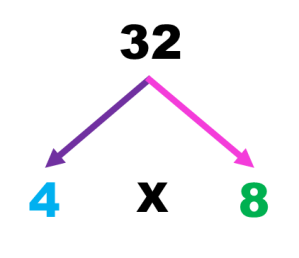
Descomponer en factores primos el 32

El 32 se puede escribir como producto de 4 x 8

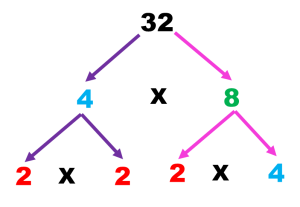
Cómo los números 4 y 8 no son primos, sigo factorizando, el 4 se representa como 2 x 2 y el 8 como 2 x 4

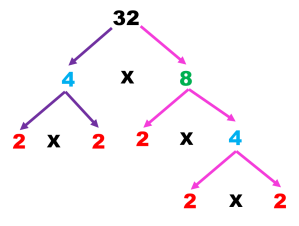
En el caso donde aparece el 2 ya no se hace nada porque es factor primo, continúo factorizando el 4 que se representa como 2 x 2

Ya tengo sólo factores primos, por lo tanto el árbol de factores de 32 se ha terminado y puede representarse por la multiplicación:

Descomponer en factores primos el 81

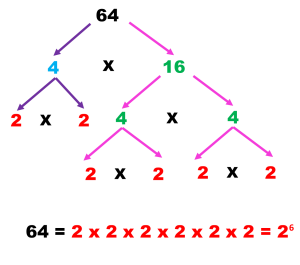
Descomponer en factores primos el 64

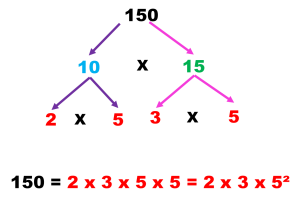
Descomponer en factores primos el 150

Ejercicios resueltos. Encontrar el mínimo común múltiplo de dos o más números

Múltiplos comunes de dos o más números

Recuerda que el múltiplo común de dos o más números, es un número que contiene exactamente a cada uno de ellos.

Cómo obtener múltiplos comunes de dos o más números

Lo practicaremos utilizando la descomposición en factores primos.
Recuerda que un factor primo es aquel que sólo es divisible entre 1 y entre sí mismo.
Puedes consultar los temas “Factorización de números” , «Descomposición de un número en factores primos» y «Mínimo común múltiplo” de este sitio para obtener más información.
Veamos ejemplos.
Encuentra el mínimo común múltiplo y los primeros cinco múltiplos comunes de 3, 4, y 8

Encuentra el mínimo común múltiplo y los primeros cinco múltiplos comunes de 2, 4, y 6

Encuentra el mínimo común múltiplo y los primeros cinco múltiplos comunes de 7 y 10

Todos los números son múltiplos de 1.
Cada número es múltiplo de sí mismo.
Encuentra todos los números que tienen como múltiplo común el 20.

Encuentra todos los números que tienen como múltiplo común el 60

Encuentra todos los números que tienen como múltiplo común el 18

Descomposición de un número en factores primos

Descomposición de un número en factores primos

«Todo número compuesto es igual a un producto de factores primos»
Para descomponer un número compuesto en sus factores primos, se divide el número dado por el menor de sus divisores primos, el cociente se divide también por el menor de sus divisores primos y así sucesivamente con los demás cocientes hasta hallar un cociente primo que se dividirá por sí mismo y dará como cociente 1.
Ejemplo. Descomponer 84 en sus factores primos
Se divide por 2 el 84
Escribimos abajo del 84 el cociente 42 (resultado de la división anterior)
Dividimos ahora el 42 por 2 y su cociente 21 se anota abajo de él
Ahora dividimos el 21 por 3 y su cociente 7 se anota abajo de él(el 21 no es divisible por 2 exactamente por eso se divide entre 3).
El 7 es número primo, por ello no se puede dividir por 2, por 3 ni por 5.
Por lo tanto lo dividimos entre sí mismo, es decir 7 entre 7 y su cociente 1 se anota abajo de él.
Como el número 84 ya tienen como cociente al 1, hemos terminado de factorizarlo.
La descomposición en factores primos del 84 es: 84  = 2 x 2 x 3 x 7 = 2² x 3 x 7


Haz clic sobre la imagen para verla más grande.

Puedes ver un método rápido para obtener factores primos de un número en este sitio.

Factorización de números.

Factorización de números

Fig. Factorización

Factorizar un número significa descomponerlo en sus factores primos , que como vimos anteriormente son los que solamente son divisibles por ellos mismos y la unidad.
Los números primos se pueden obtener a través de la Criba de Eratóstenes que es una tabla con una serie numérica en la cual se van tachando los multiplos de 2, 3, 4, 5, 6, etc…a partir de sus cuadrados.
Se llama «criba» porque al tachar los números se van formando como agujeros y de «Eratóstenes» porque fue este célebre matemático griego el creador de este procedimiento. 
Números primos Ver explicación
Recordemos que los números primos de la serie numérica del 1 al 150 son:
1,2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139 y 149.
Para conocer si un número es primo o no, se divide dicho número por todos los números primos menores que él y si se llega, sin obtener cociente exacto, a una división inexacta en la que el cociente sea igual o menor que el divisor, el número dado es primo. Si una división es exacta, el número dado no es primo.

Múltiplos, divisores y factores

Múltiplos

«Un múltiplo de un número es el que lo contiene un número entero de veces.
Ejemplo.
        12 es múltiplo de 2 porque 12 contiene 6 veces al 2
        Los primeros múltiplos del 1 al 10 suelen agruparse en lo que llamamos tablas de multiplicar.
        Los múltiplos de 2 son: 2, 4, 6, 8, 10, 12, 14, etc…
Divisores

«Un divisor es cada uno de los factores en los que se puede descomponer un número y que lo dividen exactamente
Ejemplo.
        5 es divisor de 15 porque 15 lo contiene 3 veces
        Los múltiplos de 5 son: 5, 10, 15, 20, 25, 30, 35, etc…

Factores

«Un factor es una cantidad que se multiplica por otra para hallar el producto.
Ejemplo.
        4 y 2 son factores de 8 porque 4 x 2 = 8