Números naturales y números decimales. Sucesores.

¿Cuál es el sucesor?

En este ejercicio vamos a representar pares de números naturales (1, 2, 3, 4, 5, 6…etc.), en rectas numéricas, e identificar un tercer número natural que se pueda ubicar entre los dos primeros.
a) Ubiquemos 6 y 8, y entre ellos un tercer número natural.

Observa que el único número natural que puedes ubicar entre 6 y 8, es 7.

Como puedes ver, en la recta sólo ubiqué los números naturales pedidos, pero también puedes colocar los números del 1 al 10, y ubicar los que se solicitan. O los números que tú desees, siempre y cuando consideres al 6 y al 8 y entre ellos, al 7.

b) 4 y 5

Entre estos dos números no hay otro número natural que se pueda ubicar. Después del 4 siempre está el 5.
Ahora vamos a representar en la recta numérica los números decimales indicados, e identificar entre ellos, un tercer número decimal.

Hay un número infinito de números decimales que se pueden ubicar entre los dos dados, ya que cada parte que va resultando, se puede siempre dividir en diez partes iguales. Podemos empezar por ubicar cualquiera de estas diez partes en la que dividimos la distancia que hay entre 1.2 (que equivale a 1.20) y entre 1.3 (que equivale a 1.30).
a) 1.2 y 1.3

También puedes ubicar estos números decimales.

b) 1.23 y 1.24

O también puedes dividir uno de esos décimos, en diez partes iguales y ubicar otro número decimal.

Con base en las actividades anteriores, podemos decir que:
1. El sucesor de 6 siempre es 7
2. Todos los números naturales tienen un sólo sucesor.
Porque al aumentar una unidad a cualquier número natural, sólo puede resultar un número (ejemplo 6 + 1 =7), no existe otro número natural que resulte de esta suma.
3. El 1.2 no tiene sucesor,
4. Los números decimales no tiene sucesor.
5. Después de un número decimal, la cantidad de números decimales que hay, es infinita.
6. Esta propiedad de los números decimales se conoce como propiedad de densidad.

Desafío 4. Quinto grado

Desafío 4. Anticipo el resultado

En este desafío vas a reafirmas los aprendizajes que adquiriste en el desafío 3.
Practica lo aprendido.
Da clic en el siguiente tema para aclarar dudas.
«La división y la división abreviada»

O puedes revisar la información del «Desafío 3. Quinto grado«

Divisores de uno o más números. Método rápido para hallarlos

 Cómo hallar los divisores rápido

EJERCICIOS RESUELTOS. DIVISORES DE UN NÚMERO. MÉTODO PARA HALLARLOS.
El método utilizado en estos ejercicios es el árbol de factores.
Resuelvo un ejemplo paso a paso.
Encontrar los divisores de 32.
1. Realizo el árbol de factores, que consiste en representar el 32 con dos factores que multiplicados den como resultado 32. Voy a iniciar con los factores 4 x 8 = 32, aunque pueden ser otros dos factores que multiplicados den 32.

2. Encuentro dos factores que multiplicados den 4 y otros dos que den 8. Recuerda que NO PUEDES UTILIZAR EL 1 (1 x 4 ó 1 x 8), por ello, el 4 sólo puede representarse con los factores 2 x 2. El 8 queda como 2 x 4.

3. En el caso del 4 he llegado a los factores primos (que sólo se dividen por 1 y por sí mismos) por lo que ya no hay más factores (están encerrados en círculo rojo). En el caso del 8, el factor 2 también es primo (encerrado en círculo rojo), así se queda; pero en el caso del 4 aún puedo obtener factores: 2 x 2.

4. Como en el caso de los dos factores iniciales: 4 x 8 ya he llegado a los factores primos, he terminado de factorizarlos.
Para saber cuántos divisores tiene el 32 voy a representar al 32 con factores primos (los que están encerrados en círculos rojos) en su forma abreviada. En este caso sólo está el factor primo 2 y aparece 5 veces, es decir que el 32 se representa así:

Con la representación 2⁵ (dos a la quinta potencia) voy a saber cuántos divisores tiene el 32 sumando una unidad al exponte 5 de su forma abreviada, es decir 5 + 1 = 6; por lo que el 32 tiene seis divisores.

Ahora, para obtener los seis divisores de 32 voy a utilizar una tabla como la siguiente:

5. En esta tabla organizo los números obtenidos en el árbol de factores.
6. Registro los números que se derivan del factor de la izquierda 4 (que en este caso escribí con azul), antes de la línea vertical de la tabla, en forma vertical. Si hay factores que se repiten, como es el caso del 2, sólo los escribo una vez. Y todos los factores que proceden del factor de la derecha 8 (que en este caso escribí con verde), los escribo sobre la línea horizontal de la tabla, en forma horizontal


7. Ahora multiplico cada factor vertical por cada factor horizontal, escribiendo debajo los resultados.

8. Los divisores de 32 están en la tabla. Organízalos y escríbelos de menor a mayor sin repetirlos y agregando el 1, ya que éste es divisor de todos los números.

Otros ejemplos:

a) Encontrar los divisores de 64

b) Encontrar los divisores de 81

b) Encontrar los divisores de 81.

c) Encontrar los divisores de 18

En este ejemplo vamos a observar que el resultado de la factorización puede tener más de un factor (2 y 3 en este caso). Aquí hay que sumar una unidad a cada exponente y multiplicar los resultados de las sumas. Cuando un factor primo aparece sólo una vez, se considera que está a la primera potencia, es decir que su exponente es 1.

d) Encontrar los divisores de 56

e) Encontrar los divisores de 120

En este ejemplo vamos a ver que hay ocasiones que en la tabla que se realiza no aparecen todas las parejas de los divisores que multiplicados dan el número original (en este caso 120), pero sin embargo, si aparecen los factores con los que se pueden encontrar. Veamos el ejemplo por pasos:





Como puedes ver, en la tabla sólo aparecen 14 de los 16 divisores que tiene el 120. Para encontrar los que faltan sólo tienes que ordenar por parejas, los números de la tabla que multiplicados entre sí, dan 120.

6. Divide el número original por los factores que no tienen pareja para encontrar los divisores que faltan (en este caso 3 y 15). Así tendrás el total de divisores de 120

f) Veamos otro ejemplo:

 Encontrar los divisores de 624

Ejercicios resueltos. Descomposición de un número en factores primos. Método rápido. Árbol de factores

Factores primos

El factor es un número que puede dividir a otro sin residuo, es decir, exactamente.
Ejemplo: Los factores de 16 son 1, 2, 4, 8 y 16 porque:

Un factor es primo cuando sólo puede dividirse por sí mismo y por la unidad. Ejemplo:

Para obtener los factores primos de un número se pueden utilizar dos métodos: la descomposición por divisiones sucesivas en tabla y la descomposición a través del árbol de factores.
El método de la descomposición por divisiones sucesivas en tabla lo explico en el tema: Descomposición de un número en factores primos de este sitio.
Aquí voy a explicar el método del árbol de factores, que es un diagrama en el que se muestran los factores primos de un número.
Es un método rápido pero debes cumplir con los siguientes requisitos:
a) En las ramas del árbol nunca puedes escribir el 1.
b) Si al querer elaborar el árbol de factores de un número sólo tienes como factores al 1 y al mismo número, entonces el número original es un número primo y no se puede hacer el árbol de factores.
Ejemplo: El 13 sólo puede dividirse entre 1 y entre sí mismo, por ello no puede realizarse el árbol de factores.
c) Cuando escribes números primos en un árbol, éstos ya no se factorizan.
Ejemplo: El árbol de factores del 9 es 3 x 3 y como el 3 es factor primo, así se queda

d) El resultado se queda representado como árbol o puedes indicarlo como una multiplicación de factores.

Veamos ejemplos con diferentes números.

Descomponer en factores primos el 32

El 32 se puede escribir como producto de 4 x 8

Cómo los números 4 y 8 no son primos, sigo factorizando, el 4 se representa como 2 x 2 y el 8 como 2 x 4

En el caso donde aparece el 2 ya no se hace nada porque es factor primo, continúo factorizando el 4 que se representa como 2 x 2

Ya tengo sólo factores primos, por lo tanto el árbol de factores de 32 se ha terminado y puede representarse por la multiplicación:

Descomponer en factores primos el 81

Descomponer en factores primos el 64

Descomponer en factores primos el 150

Ejercicios resueltos. Problemas que utilizan el mínimo común múltiplo

Problemas que se resuelven con el mínimo común múltiplo

1.- Para comprar un juego, la hermana de Juan aportó 1/6 del total del precio, su mamá aportó 1/5, su papá 2/4 y el resto Juan. ¿Qué parte del costo aportó Juan? Si pagaron $120.00, ¿Cuánto aportó cada uno?

2.- ¿Con qué cantidad menor que $40.00 podré comprar un número exacto de chocolates de $4.00, $6.00 y $9.00?

3.- ¿Cuál es la menor suma de dinero que se puede tener en billetes de $20.00, de $50.00 y de $100.00 y cuántos billetes de cada denominación harían falta en cada caso?

4.- Hallar la menor distancia que se puede medir exactamente con una regla de 2, de 5, y de 8 pies de largo.

5.- ¿Cuál es la menor capacidad de un estanque que se puede llenar en un número exacto de minutos por cualquiera de tres llaves que vierten: la primera 12 litros por minuto, la segunda 18 litros por minuto, y la tercera 20 litros por minuto?

6.- Tres aviones salen a la misma hora de un mismo aeropuerto, el primero sale cada 8 días, el segundo cada 10 días, y el tercero cada 20 días. Si salen el 2 de enero, ¿cuáles serán las dos fechas más próximas en que volverán a salir juntos? (el año es de 365 días).

7.- La señora Clara tiene que tomar tres medicamentos, el primero cada 6 horas, el segundo cada 8 horas y el tercero cada 12 horas. Si la primera toma de los tres medicamentos la hace al mismo tiempo, ¿Cuánto tiempo tendrá que pasar para que vuelva a tomar los tres medicamentos juntos?

Al cumplir tres días con el tratamiento, cuántas veces ha coincidido la toma simultánea de los tres medicamentos?

Después de la primera toma, cuántas horas deben transcurrir para que ocurra otra toma simultánea de al menos dos medicamentos?

R= 12 horas, medicamentos de cada 6 horas y cada 12 horas.

Ejercicios resueltos. Encontrar el mínimo común múltiplo de dos o más números

Múltiplos comunes de dos o más números

Recuerda que el múltiplo común de dos o más números, es un número que contiene exactamente a cada uno de ellos.

Cómo obtener múltiplos comunes de dos o más números

Lo practicaremos utilizando la descomposición en factores primos.
Recuerda que un factor primo es aquel que sólo es divisible entre 1 y entre sí mismo.
Puedes consultar los temas “Factorización de números” , «Descomposición de un número en factores primos» y «Mínimo común múltiplo” de este sitio para obtener más información.
Veamos ejemplos.
Encuentra el mínimo común múltiplo y los primeros cinco múltiplos comunes de 3, 4, y 8

Encuentra el mínimo común múltiplo y los primeros cinco múltiplos comunes de 2, 4, y 6

Encuentra el mínimo común múltiplo y los primeros cinco múltiplos comunes de 7 y 10

Todos los números son múltiplos de 1.
Cada número es múltiplo de sí mismo.
Encuentra todos los números que tienen como múltiplo común el 20.

Encuentra todos los números que tienen como múltiplo común el 60

Encuentra todos los números que tienen como múltiplo común el 18

Ejemplos resueltos. Máximo común divisor.

Problemas resueltos con máximo común divisor

Si no te quedan claros los ejercicios, te invito a que revises el tema “Máximo común divisor” en este sitio. Allí encontrarás todo lo relacionado con el tema.
Aquí te expongo algunas de las situaciones donde se utiliza para la solución de las mismas.
Recordemos que el máximo común divisor de dos o más números, es el mayor número que los divide a todos exactamente.
Veamos ejemplos en los que se utiliza.
1.- Se quiere cubrir un piso rectangular de 450 cm de largo y 360 cm de ancho con losetas cuadradas de igual medida. No se vale hacer cortes, es decir, el número de losetas tendrá que ser un número entero.
a) Escribe tres medidas que pueden tener las losetas para cubrir todo el piso.
b) ¿Cuál es la medida mayor?
Solución:
Busco el máximo común divisor de 450 y 360 por descomposición en factores primos.

El m.c.d. de 450 y 360 es 90. Esto indica que 90 es el número mayor en el que se pueden dividir los dos números. Y para el caso del problema, indica que es la medida mayor que pueden tener las losetas cuadradas: 90 x 90.
Si divido 450 entre 90 y 360 entre 90, obtengo la cantidad de losetas que utilizaría:

Se me pide que dé tres medidas que podrían tener las losetas.
Ahora obtengo todos los divisores compuestos de 90, que serán también divisores de 360 y 450:

Y con ellos obtengo las medidas que pueden tener las losetas:

Las respuestas del problema serían:
a) Escribe tres medidas que pueden tener las losetas para cubrir todo el piso.
90 x 90, 45 x 45, 30 x 30, 18 x 18, 15 x 15, 10 x 10, 9 x 9 etc.
b) ¿Cuál es la medida mayor?
90 x 90
 Problema 2.-

En la ferretería tienen dos tambos de 200 litros de capacidad. Uno contiene 150 litros de alcohol y el otro 180 litros de aguarrás. Se decidió mandar hacer varios garrafones del mismo tamaño y capacidad para envasar tanto el alcohol como el aguarrás sin que sobre nada de líquido en los tambos.
a) ¿Es posible que la capacidad de los garrafones sea entre 10 y 20 litros?
b) Escribe tres capacidades diferentes que pueden tener los garrafones.
Antes de ordenar la fabricación de los garrafones, llegó a la ferretería un tercer tambo con 105 litros de cloro. Ahora se necesita que los tres líquidos sean envasados en garrafones con el mismo tamaño y capacidad.
c) Escribe dos capacidades diferentes que pueden tener los garrafones.
d) ¿Cuál será el de mayor capacidad?
Resolvamos la primera parte. Hay que obtener el m.c.d. de 150 y 180:

Ahora obtengo todos los divisores compuestos de 30, que serán también divisores de 150 y 180:

Con esta información contesto las preguntas a y b:
a) ¿Es posible que la capacidad de los garrafones sea entre 10 y 20 litros?
Si. Los garrafones pueden ser de 10 ó 15 litros

b) Escribe tres capacidades diferentes que pueden tener los garrafones.
De 30 litros, de 15 litros, 10 litros, 6 litros, etc…
Resolvamos la segunda parte.
Hay que obtener el m.c.d. de 30 (por ser el máximo común divisor de 150 y 180) y de 105 que son los litros de cloro:

Y obtener los divisores compuestos de 15:

Contestamos las preguntas c y d:
c) Escribe dos capacidades diferentes que pueden tener los garrafones.
15 litros, 5 litros, 3 litros, 1 litro
d) ¿Cuál será el de mayor capacidad?
15 litros
Problema 3.-

 ¿Se podrán dividir tres varillas de 20 cm, 24 cm y 30 cm en pedazos de 4 cm sin que sobre ni falte nada en cada varilla?

No. El máximo común divisor de los tres números es 2. 30 no es múltiplo de 4.

Problema 4.-

Un padre da a un hijo $80, a otro $75 y a otro $60 para repartir entre los pobres, de modo que todos den a cada pobre la misma cantidad. ¿Cuál es la mayor cantidad que podrán dar a cada pobre y cuántos los pobres socorridos?
La mayor cantidad es $5 y serán socorridos 43 pobres

Problema 5.-

Dos cintas de 36 metros y 48 metros de longitud se quieren dividir en pedazos iguales y de la mayor longitud posible. ¿Cuál será la longitud de cada pedazo?

Sucesión geométrica

Sucesión geométrica

Es un conjunto de números llamados términos, en el cual el cociente entre dos términos consecutivos siempre es el mismo, es la regularidad de la sucesión
Observa la siguiente sucesión:
½, 2, 8, 64…
Estos números reciben el nombre de términos, es decir que en esta secuencia o progresión geométrica tengo 4 términos.

Los términos consecutivos son los que están juntos:
½ y 2 son términos consecutivos.
2 y 8 son términos consecutivos.
8 y 64 son términos consecutivos, etc.
El cociente entre dos términos consecutivos siempre es el mismo y recibe el nombre de razón de la sucesión geométrica.
La razón se obtiene dividiendo cada término por su antecesor. En la sucesión anterior quedaría así:

Por lo tanto, la razón de esta sucesión es 4.
Si te piden el término que sigue en la sucesión, tendrás que multiplicar el último término por cuatro, siendo la respuesta el número 128.
Como en la sucesión aritmética, también en esta sucesión puedes utilizar una fórmula para obtener los términos que se te solicita. A veces los ejercicios son sencillos y los puedes ir obteniendo fácilmente, pero en otras, o es más complicado, o te solicitan términos muy lejanos a los que estás trabajando, por ejemplo tienes cuatro términos y te piden el término cincuenta. En estos casos la fórmula te será de mucha utilidad.
En esta fórmula se trabaja con potencias, es decir, un número se multiplica por sí mismo varias veces.
Por ello vamos a recordar cómo se trabaja con ellas.
Si tengo un número elevado a la cero potencia, el resultado es 1.
4° = 1, 12° = 1, 2° = 1
Si tengo un número elevado a la primera potencia, el resultado es el mismo número.
4¹ = 4, 12¹ = 12, 2¹ = 2
Si tengo un número elevado a la segunda potencia, la base se multiplica por si dos veces
4² = 4 x 4 = 14, 12² = 12 x 12 = 144, 2² = 2 x 2 = 4
Si tengo un número elevado a la tercera potencia, la base se multiplica por sí misma tres veces
4³ = 4 x 4 x 4 = 64, 12³ = 12 x 12 x 12 = 1728, 2³ = 2 x 2 x 2 = 8
Es decir que el exponente (el número pequeño que aparece en la parte superior derecha) te indica cuántas veces vas a multiplicar la base (el número que tiene el exponente) por sí misma.
Ahora pasemos a la fórmula para los términos de la sucesión geométrica. Es la siguiente:

a por r a la n potencia menos 1.

En donde a es desconocido, r es la razón del segundo término entre el primero, y n es el término.

Observa el ejemplo 1 ejemplo.
Escribe los ocho primeros términos de la sucesión siguiente:

Primero obtenemos la razón del segundo término entre el primero:
6 ÷ 3 = 2
Y con este dato empiezo a trabajar con la fórmula.

Sustituyo en la fórmula r por el valor de la razón, n por el 1 que equivale al primer término y como resultado pongo el primer número de la sucesión:

Ahora realizo la resta indicada en el exponente:

Date cuenta que el resultado es una base elevada a la cero potencia, por lo que el resultado es 1

Al multiplicar a por 1 el resultado es a, por lo que su valor es 3:

Con este resultado puedo obtener todos los términos de la sucesión que desee. Veamos:
Para encontrar el valor del segundo término, sustituyo n por 2:

Y ya tengo el segundo término.
Para obtener el tercer término, sustituyo n por 3; y así continúo hasta obtener los ocho términos solicitados:

La sucesión sería ésta:

Como esta sucesión es sencilla, puedes realizarla fácilmente al ir multiplicando por 3 cada término. Pero si sólo te pidieran el término 15, sería muy tediosos estar realizando todas las multiplicaciones hasta llegar a la de 15. Con la fórmula es más sencillo, sólo sustituyes n por 15:

El término 15 de esta sucesión sería:

Mientras las sucesiones sean sencillas, puedes resolverlas sin fórmula.
Ejemplo 2:
Completa la siguiente sucesión:

Obtengo la razón dividiendo el segundo término entre el primero. La razón es 4, por ello voy a ir multiplicando cada término por 4:

Ejemplo 3.
Qué términos faltan en la siguiente sucesión:

La razón entre el segundo término y el primero es 28 ÷ 4 = 7
Multiplico cada término por 7.

Para determinar si un número pertenece o no a una sucesión geométrica basta con identificar la razón de dos términos consecutivos y después ir multiplicando o dividiendo (según sea el caso) cada término por la razón encontrada hasta llegar al número dado.
Si al multiplicar un término por la razón, el resultado es mayor que el dado, este número no será término de la sucesión dada.
Ejemplo 4.
Tenemos la siguiente serie:

Los números 19 683 y 25 789 ¿pertenecen a esta sucesión?
Primero encuentro la razón del segundo término entre el primero:

Sabiendo que la razón es 3 , es decir que cada término anterior se va multiplicando por 3 para obtener al siguiente, empiezo a multiplicar el último término dado por 3 y así sucesivamente hasta comprobar si es término o no de la sucesión:

Como puedes ver, el número 19 683 si resulta de multiplicar un término de la sucesión por 3, por lo tanto, si forma parte de la sucesión.
Y el número 25 789 no pertenece a la sucesión, ya que en la siguiente multiplicación podemos ver que resulta 59 049 y éste número es mayor que 25 789.
El número 19 683 ocupa el octavo lugar de la sucesión dada.
Ejemplo 5.
Con base en las siguientes figuras contesten lo que se pide. Consideren como unidad de medida el cuadro:

a) ¿Cuál es la sucesión numérica que representa las áreas de los triángulos?
b) ¿Cuál será el área de los triángulos en las figuras 6, 7 y 8?
Primero identifico las áreas del primero y segundo triángulos, éstos serán los términos primero y segundo de la sucesión. El primero tiene un área de ½ unidad y el segundo 2 unidades. Por lo tanto la serie inicia así:

Ya tengo el primero y el segundo término de esta sucesión.
Ahora encuentro la razón del segundo término entre el primero:

Trabajo con la fórmula sustituyendo valores para obtener el de a. r es igual a 4, n es igual a 1, y el resultado es el valor del primer término: ½

El valor de a es ½ ó 0.5
Ahora que ya tengo todos los valores de la fórmula, puedo obtener los términos de la serie que me piden:

La sucesión de números que corresponde a las áreas de las figuras es:

Las áreas de los triángulos en las figuras 6, 7 y 8 es:

Medidas de tendencia central

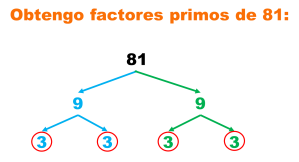
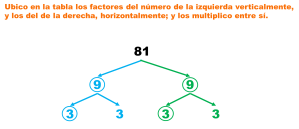
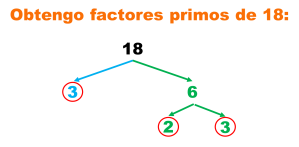
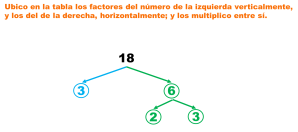
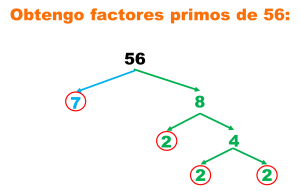
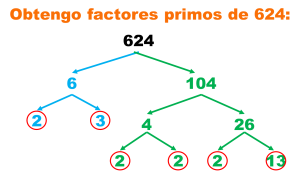
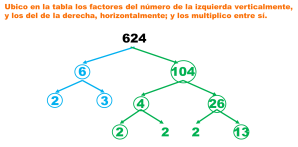
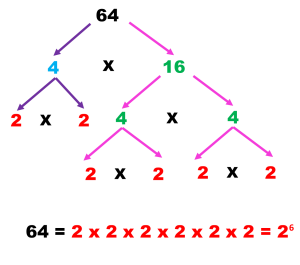
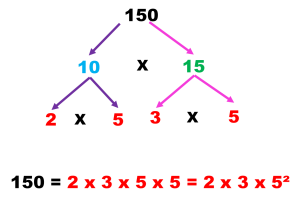
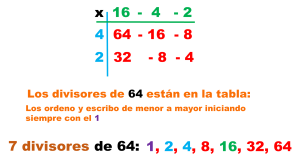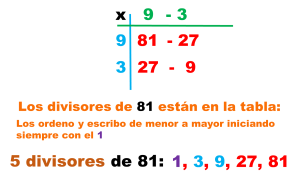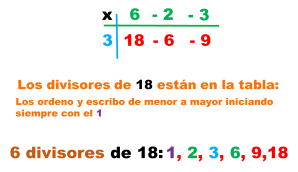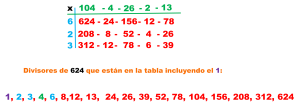Medidas de tendencia central

Son medidas que se utilizan en la estadística para resumir información.

Para poderlas realizar se necesita una situación en la que se presentan varios datos (valores).

Estos datos pueden o no repetirse y a las veces que se repite un dato, se le conoce como frecuencia.
Las medidas de tendencia son tres:
a) Media o promedio
b) Moda
c) Mediana

Media aritmética o promedio

Consiste en hallar un número medio entre varios de la misma especie.
Es una cantidad que nos indica la cantidad total dividida en partes iguales.

Se identifica con las letras M o X
Para hallar la media aritmética o promedio de varias cantidades, se suman y esta suma se divide por el total de las cantidades.
Ejemplo:
Hallar la media aritmética o promedio de las siguientes cantidades (estos son los datos o valores):

9, 10, 4, 6, 9, 6, 8, 9, 1, 9, 6, 9, 4

Primero sumo todas las cantidades anteriores. El resultado es 90
El resultado de la suma se divide entre el total de los números sumados:

9 +10 + 4 + 6 + 9 + 6 + 8 + 9 + 1 + 9 + 6 + 9 + 4 = 90

90 ÷ 13 = 6.923

Por lo tanto, la media aritmética o promedio de los datos o valores anteriores es 6.923

M=6.923      o    X = 6.923

El promedio o media aritmética no siempre es el valor representativo de  una situación estadística.

A veces los valores no están distribuidos normalmente, es decir, hay situaciones en las que los  valores son exageradamente mayores o menores con relación a la mayoría; y esto hace que el promedio salga muy alto con relación a los demás y no es un dato realista.

En estos casos, es recomendable utilizar la moda o la mediana como medida representativa de la situación.

Moda

Esta medida consiste en encontrar dato o valor que se repite más veces en el conjunto de valores dados. Es decir, el valor que tiene mayor frecuencia.

Se identifica con las letras Mo
Ejemplo:
En el conjunto

9, 10, 4, 6, 9, 6, 8, 9, 1, 9, 6, 9, 4

la moda es 9 porque es el valor con mayor frecuencia (el que más se repite). Mo = 9

Si en un grupo de datos o valores hay dos con la misma frecuencia, entonces se dice que es bimodal.

Ejemplo:

En el conjunto 9, 10, 4, 6, 9, 6, 8, 9, 1, 9, 6, 9, 4, 6, 6

La frecuencia de 9 y 6 es igual (cinco veces cada uno)  y es la mayor (es decir los valores que más se repiten), por lo tanto es bimodal.

Mo bimodal = 9 y 6

Si hubiera más de tres datos con la mayor e igual frecuencia, entonces sería multimodal.

Por ejemplo: En el conjunto anterior que hubiera tres cuatros más, entonces, el 9, el 6 y el 4 tendrían la misma frecuencia y la más alta, por lo tanto la moda sería multimodal.

9, 10, 4, 6, 9, 6, 8, 9, 1, 9, 6, 9, 4, 6, 6, 4, 4, 4

Mo multimodal = 9, 6, 4

Lo importante es que sea el o los valores que más se repiten.

La moda es representativa de una situación estadística cuando se busca lo que ocurre con mayor frecuencia.

Mediana

Consiste en hallar el valor que se encuentra en el centro del conjunto de datos o valores. Para encontrarla, la condición es que los datos estén ordenados del menor al mayor.

Se identifica con las letras Md

Se pueden dar dos casos.

1.- Cuando el número total de valores es impar.

En este caso, después de ordenar los valores de menor a mayor, la mediana es el valor que queda al centro de la serie.
Ejemplo:
Encontrar la mediana del conjunto:

9, 10, 4, 6, 9, 6, 8, ,9, 1, 9, 6, 9, 4

Primero hay que ordenarlos de menor a mayor:

1, 4, 4, 6, 6, 6, 8, ,9, 9, 9, 9, 9, 10

Son trece valores, el trece es impar.

Ahora, localizar el que se encuentra en el centro. quedan seis datos antes del centro y seis después.

1, 4, 4, 6, 6, 6, 8, 9, 9, 9, 9, 9, 10

La mediana de este conjunto es 8.

Md = 8

2.- Cuando el número total de valores es par.

En este caso se localizan los dos valores que quedan al centro, se suman y el resultado se divide entre dos (es decir, se promedian los dos valores) para encontrar la mediana.

Ejemplo. En el conjunto 9, 10, 4, 6, 9, 6, 8, ,9, 1, 9, 6, 9, 4, 6

Los datos del conjunto son catorce (que es número par), entonces ordeno de mayor a menor y busco los dos que quedan al centro de la serie

1, 4, 4, 6, 6, 6, 8, 9, 9, 9, 9, 9, 10,6

Ahora saco el promedio de 8 y 9

8 + 9 = 17 ÷ 2 = 8.5

La mediana es 8.5

Md = 8.5

La mediana es representativa de una situación estadística cuando los valores tienen varios valores con la misma frecuencia y varios valores comparativamente extremosos, ya sea bajos o altos con relación a los demás.

La mediana deja a la mitad de valores más pequeños a su izquierda y a la mitad de datos más grandes a su derecha.

Es más representativa porque indica que por lo menos el 50% de los datos son más pequeños que ella y el otro 50% es mayor.

Cuando tenemos información relacionada con un tema, ésta se puede organizar en tablas de frecuencia para poder obtener las medidas de tendencia central vistas anteriormente.
Veamos un ejemplo:

En la ciudad de Atlixco, Puebla, existen tres empresas textiles, de las cuales se tomó una muestra de 15 empleados de cada una para investigar sus salarios en pesos. La siguiente tabla muestra los resultados:

Lo primero que tengo que hacer es organizar los datos de menor a mayor y escribir la frecuencia con la que se presenta cada salario, en cada una de las empresas:

Con la información ordenada, puedo realizar la suma de los salarios de cada una de las empresas y dividirla entre el total de empleados para obtener el promedio:

También puedo obtener la moda de cada una de las empresas. El 1000 es la moda de la primera empresa ya que se repite cuatro veces, el 600 la de la segunda, se repite seis veces, y el 1400 la de la tercera, se repite siete veces:

Y por último puedo encontrar la mediana. En la primera empresa el dato que queda al centro es $1000, en la segunda empresa el dato es $900 y en la tercera es $ es $1400.

La mediana de las tres empresas, sabiendo que son 45 datos (15 de cada empresa), el centro estará en el número 23. Si sumo el total de veces que se repite cada salario, me doy cuenta que el 23 estará en el salario $1400

Esto lo puedes comprobar escribiendo los 45 salarios y señalando el que se encuentra en el lugar 23:

Sucesión aritmética

 Sucesión aritmética 

Es un conjunto de números llamados términos, en el cual la diferencia entre dos términos consecutivos siempre es la misma, es la regularidad de la sucesión
Observa la siguiente sucesión:

2, 4, 6, 8, 10…

Estos números reciben el nombre de términos, es decir que en esta secuencia aritmética tengo 5 términos:

2, 4, 6, 8, 10…
1, 2, 3, 4, 5…

Los términos consecutivos son los que están juntos:
2 y 4 son términos consecutivos.
4 y 6 son términos consecutivos.
6 y 8 son términos consecutivos, etc.
La diferencia entre dos términos consecutivos siempre es la misma, es la regularidad de la sucesión aritmética.
4 – 2 = 2
6 – 4 = 2
8 – 6 = 2
10 – 8 =2

Veamos otro ejemplo:

3, 6, 12, 24, 48…

La diferencia entre dos términos consecutivos NO es la misma,
6 – 3 = 3
12 – 6 = 6
24 – 12 = 12
48 – 24 =24

IMPORTANTE:
SI LA REGULARIDAD DE LA SUCESIÓN NO ES UNA SUMA O DIFERENCIA SIEMPRE IGUAL, ENTONCES NO ES UNA SUCESIÓN ARITMÉTICA, SINO UNA SUCESIÓN GEOMÉTRICA; Y ES OTRO TEMA QUE EXPLICAREMOS DESPUÉS.
En esta ocasión nos enfocaremos a la sucesión aritmética.
Observa los siguientes ejemplos:

Ejemplo 1.
Si una sucesión aumenta de 7 en 7, ¿cuáles son los primeros 10 términos si inicia en 4?
Los términos son los números que cumplen con la condición de ir aumentando de 7 en 7.
Si me piden los diez primeros términos, iniciando por el 4, a partir de éste voy ir sumando 7 a cada número.
4 + 7 = 11, 11 + 7 =18, 18 + 7 = 25, etc.
Los 10 primeros números de la sucesión aritmética son:

4,  11, 18, 25, 32, 39, 46, 53, 60, 67
1    2    3    4    5     6    7    8   9    10

Los números 1, 2, 3, 4, 5, 6, 7, 8, 9, 10; representan a los términos.
Si me preguntan cuál es el término 5, diría que es 32; si me preguntan por el término 2, diría que es 11; si me preguntan por el término 7, diría que es 46; etc.
Los términos consecutivos son los que están juntos.
18 y 25 son dos términos consecutivos, entre ellos debe haber 7 unidades de diferencia. 25 – 18 = 7. Esta diferencia de 7 es la regularidad.
46 y 53 son dos términos consecutivos, entre ellos debe haber 7 unidades de diferencia. 46 – 53 = 7. Esta diferencia es la regularidad
32 y 39 son dos términos consecutivos, entre ellos debe haber 7 unidades de diferencia. 39 – 32 = 7. Esta diferencia es la regularidad
Si me preguntan qué número será el término 15 de la serie, tendré que sumar:
67 + 7 = 74, que será el término 11;
74 + 7 = 81, que será el término 12;
81 + 7 = 88, que será el término 13;
88 + 7 = 95, que será el término 14;
95 + 7 = 102, que será el término 15;
El término pedido será el número 102.
Concluyendo:
Números de la secuencia: 4, 11, 18, 25, 32, 39, 46, 53, 60, 67……….102
Términos: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10…..15
Regularidad: Cada término se determina sumando 7 al término anterior.

Ejemplo 2.
¿Cuáles son los 10 primeros términos de una sucesión, si inicia en 9 y la diferencia entre dos términos consecutivos es 12?
Los términos son los números que cumplen con la condición de ir aumentando de 12 en 12.
Me piden los diez primeros términos iniciando por el 9, a partir de él voy ir sumando 12 a cada número.
9 + 12 = 21, 21 + 12 = 33, 33 + 12 = 45, etc.
Los 10 primeros números de la sucesión aritmética son:

9, 21, 33, 45, 57, 69, 81, 93, 105, 117
1    2    3    4    5    6    7    8      9    10

Los números 1, 2, 3, 4, 5, 6, 7, 8, 9, 10; representan a los términos.
Si me preguntan cuál es el término 3, diría que es 33; si me preguntan por el término 6, diría que es 69; si me preguntan por el término 9, diría que es 105; etc.
Los términos consecutivos son los que están juntos.
9 y 21 son dos términos consecutivos, entre ellos debe haber 12 unidades de diferencia: 21 – 9 = 12. Esta diferencia de 12 es la regularidad
105 y 117 son dos términos consecutivos, entre ellos debe haber 12 unidades de diferencia: 117– 105 = 12. Esta diferencia es la regularidad.
69 y 81 son dos términos consecutivos, entre ellos debe haber 12 unidades de diferencia: 81 – 69 = 12. Esta diferencia es la regularidad.
Si me preguntan qué número será el término 50 de la serie, tendré que sumar:
117 + 12 = 129, que será el término 11;
129 + 12 = 141, que será el término 12;
141 + 12 = 153, que será el término 13;
153 + 12 = 165, que será el término 14;
165 + 12 = 177, que será el término 15; y así sucesivamente hasta llegar a
597 que es el término 50.
El término pedido será el número 597.
Concluyendo:
Números de la secuencia: 9, 21, 33, 45, 57, 69, 81, 93, 105, 117…..597
Términos: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10………50
Regularidad: Cada término se determina sumando 12 al término anterior.

Ejemplo 3.
Si una sucesión aumenta de 1.5 en 1.5, ¿cuáles son los primeros 10 términos si el primero es 0.5?
Los términos son los números que cumplen con la condición de ir aumentando de 1.5 en 1.5
Me piden los diez primeros términos, iniciando por el 0.5, voy ir sumando 1.5 a cada número.
0.5 + 1.5 = 2, 2 + 1.5 = 3.5, 3.5 + 1.5 = 5, etc.
Los 10 primeros números de la sucesión aritmética son:

0.5,  2,  3.5,  5,  6.5,  8,  9.5,  11,  12.5, 14
   1   2     3    4     5    6     7      8       9    10

Los números 1, 2, 3, 4, 5, 6, 7, 8, 9, 10; representan a los términos.
Si me preguntan cuál es el término 1, diría que es 0.5; si me preguntan por el término 6, diría que es 6.5; si me preguntan por el término 10, diría que es 14; etc.
Los términos consecutivos son los que están juntos.
0.5 y 2 son dos términos consecutivos, entre ellos debe haber 1.5 unidades de diferencia: 2 – 0.5 = 1.5 que es la regularidad.
3.5 y 5 son dos términos consecutivos, entre ellos debe haber 1.5 unidades de diferencia: 5 – 3.5 = 1.5 que es la regularidad.
11 y 12.5 son dos términos consecutivos, entre ellos debe haber 1.5 unidades de diferencia: 12.5 – 11 = 1.5 que es la regularidad.
Concluyendo:
Números de la secuencia: 0.5, 2, 3.5, 5, 6.5, 8, 9.5, 11, 12.5, 14
Términos: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Regularidad: Cada término se determina sumando 1.5 al término anterior

Ejemplo 4.
¿Cuáles son los primeros 10 términos de una sucesión si el inicial es 2/3 y la diferencia entre dos términos consecutivos es 1/6?
Los términos son los números que cumplen con la condición de ir aumentando de 1/6 en 1/6
Me piden los diez primeros términos iniciando por 2/3, a partir de éste voy ir sumando 1/6 a cada número.
Si cambio 2/3 a fracción equivalente 4/6, me será más fácil resolver al ir aumentando 1/6
4/6 + 1/6 = 5/6, 5/6 + 1/6 = 6/6, 6/6 + 1/6 = 7/6, etc.
Los 10 primeros números de la sucesión aritmética son:

4/6, 5/6, 6/6, 7/6, 8/6, 9/6, 10/6, 11/6, 12/6, 13/6,
  1     2     3     4     5     6       7      8       9      10

Los números 1, 2, 3, 4, 5, 6, 7, 8, 9, 10; representan a los términos.
Si me preguntan cuál es el término 4, diría que es 8/6; si me preguntan por el término 5, diría que es 9/6; si me preguntan por el término 6, diría que es 10/6; etc.
Los términos consecutivos son los que están juntos.
8/6 y 9/6 son dos términos consecutivos, entre ellos debe haber 1/6 de diferencia: 9/6 – 8/6 = 1/6 que es la regularidad
12/6 y 13/6 son dos términos consecutivos, entre ellos debe haber 1/6 de diferencia: 13/6 – 12/6 = 1/6 que es la regularidad
4/6 y 5/6 son dos términos consecutivos, entre ellos debe haber 1/6 de diferencia: 5/6 – 4/6 = 1/6 que es la regularidad
Concluyendo:
Números de la secuencia: 4/6, 5/6, 6/6, 7/6, 8/6, 9/6, 10/6, 11/6, 12/6, 13/6
Términos: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Regularidad: Cada término se determina sumando 1/6 al término anterior.
Si gustas puedes simplificar las fracciones.
2/3, 5/6, 1, 11/6, 11/3, 11/2, 12/3, 15/6, 2,   2 1/6,
Te puse varios ejemplos porque me interesa que te queden bien claros cuáles son los números de la secuencia, los términos de la secuencia y la regularidad de la secuencia.
Quiero que los tengas bien claros porque te voy a explicar una fórmula con la que puedes obtener cualquier término de una secuencia aritmética, sin necesidad de realizar todas las sumas para llegar al resultado. Habrá ejercicios que podrás resolver sin la fórmula, pero otros en donde te será muy útil y es bueno que te familiarices con ella.
La fórmula es la siguiente:

a n + b =

En donde:
a = regularidad
n = términos
b =?

Observa cómo funciona la fórmula. Trabajaré con los ejemplos anteriores. Trataré de ser lo más clara posible.

Ejemplo 1.
Si una sucesión aumenta de 7 en 7, ¿cuáles son los primeros diez términos si inicia en 4?
Voy a trabajar la fórmula con los dos primeros términos de la sucesión.
Sé que el primero es 4 y el segundo es 4 + 7 = 11.
4, 11,
1 2
Despejaré la fórmula para obtener el valor de b y poder obtener los otros 8 términos de la sucesión. Como resultado se pone el primer número de la sucesión, en este caso, 4.

a n + b = 4

En donde:
a = regularidad:4 = 7
n = términos: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
b =?
Sustituyendo a por la regularidad (7), n por el primer término (1) y como resultado el valor del primer término, en este caso 4;la fórmula me queda así:

a n + b = 4
(7) (1) + b = 4
7 + b = 4
b = 4 – 7
b = – 3

Observa que el 7 pasa a la derecha de la igualdad cambiando el signo. El resultado es negativo, quiere decir que en lugar de sumar en la fórmula, se va a restar (no siempre sucede esto, ya veremos otros ejemplos). Con este valor de b = – 3, puedo obtener cualquier número de la serie utilizando la fórmula.
Ya tengo el primero y segundo términos de los 10 que me piden, ahora voy a obtener los demás con la fórmula sin el resultado 4.
Observa cómo obtener los términos 3, 4, 5, 6, 7, 8, 9 y 10:

a n + b =
(7) (3) – 3 = 18
(7) (4) – 3 = 25
(7) (5) – 3 = 32
(7) (6) – 3 = 39

Obtendré el término quince sin necesidad de todos los anteriores:

(7) (15) – 3 = 102

Ejemplo 2.

¿Cuáles son los 10 primeros términos de una sucesión, si inicia en 9 y la diferencia entre dos términos consecutivos es 12?
Con esta información tengo los dos primeros términos: 9 y 9 + 12 = 21
Obtendré la fórmula de esta sucesión aritmética.
9, 21,
1 2
Despejaré la fórmula para obtener el valor de b. Como resultado se pone el primer número de la sucesión, en este caso, 9

a n + b = 9
(12) (1) + b = 9
12 + b = 9
b = 9 – 12
b = – 3

Obtendré los demás términos:

a n + b =
(12) (3) – 3 = 33
(12) (4) – 3 = 45
(12) (5) – 3 = 57
(12) (6) – 3 = 69
(12) (7) – 3 = 81
(12) (8) – 3 = 93
(12) (9) – 3 = 105
(12) (10) – 3 = 117

Y el término 50 que se me pidió lo puedo obtener sin necesidad de tener los anteriores:

(12) (50) – 3 = 597

Ejemplo 3.
Si una sucesión aumenta de 1.5 en 1.5, ¿cuáles son los primeros 10 términos si el primero es 0.5?
El primer término es 0.5 y el segundo es 0.5 + 1.5 = 2
Obtendré con la fórmula el valor de b para esta sucesión:

a n + b = 0.5
(1.5) (1) + b = 0.5
1.5 + b = 0.5
b = 0.5 – 1.5
b = – 1

Con el valor de b obtengo los demás números de la sucesión aritmética:

a n + b =
(1.5) (3) – 1 = 3.5
(1.5) (4) – 1 = 5
(1.5) (5) – 1 = 6.5
(1.5) (6) – 1 = 8
(1.5) (7) – 1 = 9.5
(1.5) (8) – 1 = 11
(1.5) (9) – 1 = 12.5
(1.5) (10) -1 = 14

El tema de la sucesión geométrica lo veremos en otro apartado.