Cuerpos geométricos
Generalidades.
Analicemos los cuerpos geométricos siguientes:
Los cuerpos geométricos están formados por varias caras.
Pueden ser poliedros regulares, poliedros irregulares y cuerpos redondos.
Veamos algunos.
Poliedro regular?
Un poliedro es regular si sus caras son polígonos regulares iguales.
Existen cinco poliedros regulares: el tetraedro (de 4 caras), el hexaedro o cubo (de seis caras), el octaedro (de ocho), el dodecaedro (de doce) y el icosaedro (de veinte).
Veamos uno de ellos.
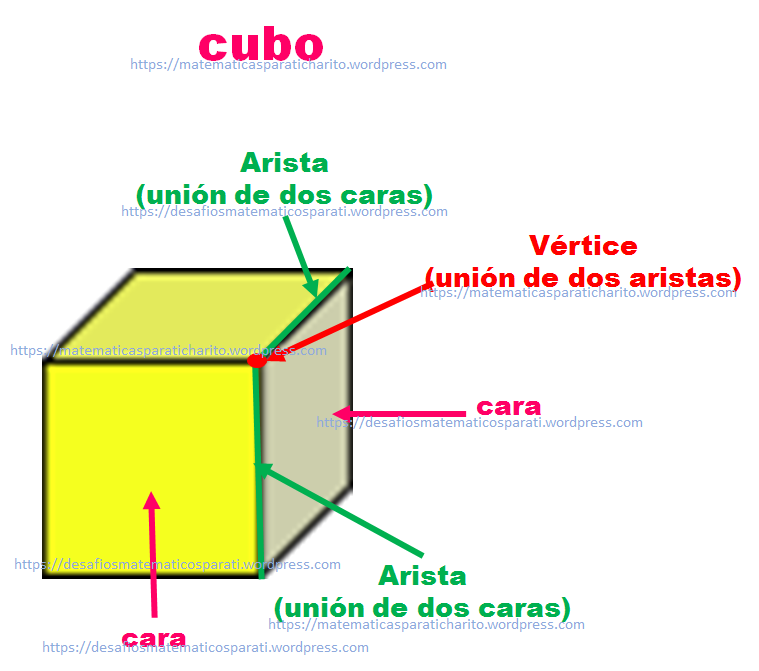
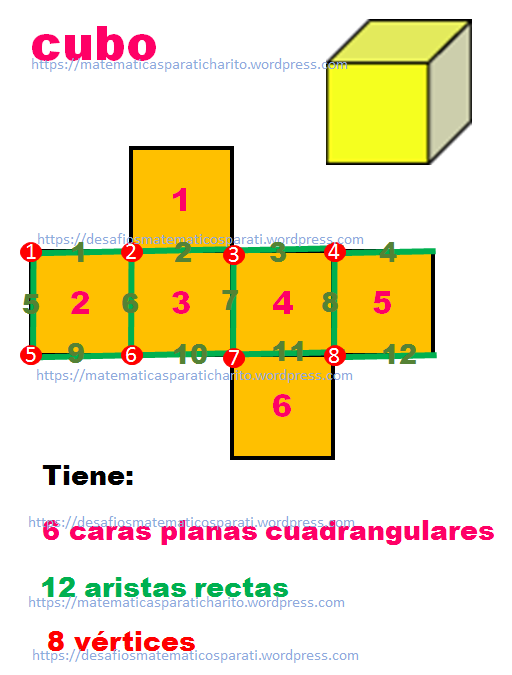
Es un cuerpo geométrico formado por seis caras planas iguales. Cada cara es un cuadrado. Tiene 12 aristas (que son las uniones de dos caras) y 8 vértices (que son los puntos donde se unen dos o más aristas).
Para elaborarlo necesitas seis cuadrados iguales.
Poliedros irregulares
Los poliedros irregulares son los prismas y las pirámides.

Es un cuerpo geométrico que tiene dos caras iguales y paralelas llamadas bases y varias caras laterales que son rectángulos.
El número de caras laterales, aristas y vértices depende de la forma que tengan sus bases.
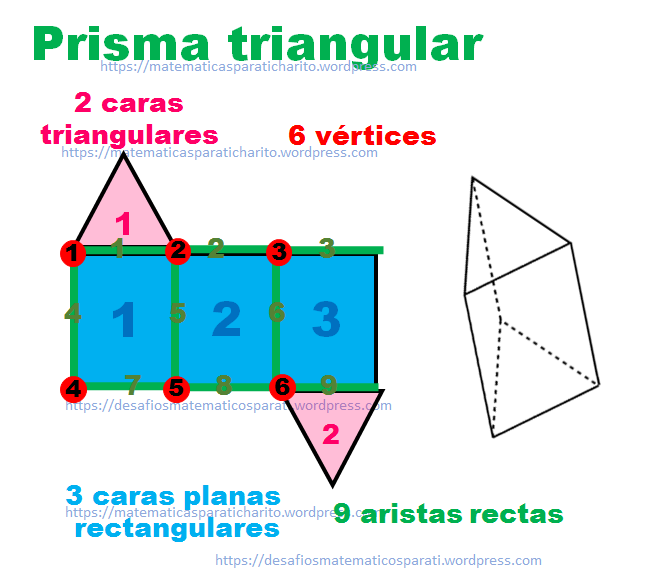
Prisma triangular. Tiene 5 caras planas, 2 de ellas triangulares que son las bases; 3 caras laterales planas rectangulares, 6 vértices y 9 aristas rectas.
Prisma cuadrangular. Tiene 6 caras planas, 2 de ellas cuadrangulares que son las bases; 4 caras laterales planas rectangulares, 8 vértices y 12 aristas rectas.

Es un cuerpo geométrico que tiene una cara llamada base y varias caras laterales triangulares.
El número de caras laterales, aristas y vértices depende de la forma que tenga su base.
Pirámide pentagonal. Tiene 6 caras planas, 1 de ellas pentagonal que es la base; y 5 caras laterales planas triangulares, 6 vértices y 9 aristas rectas.
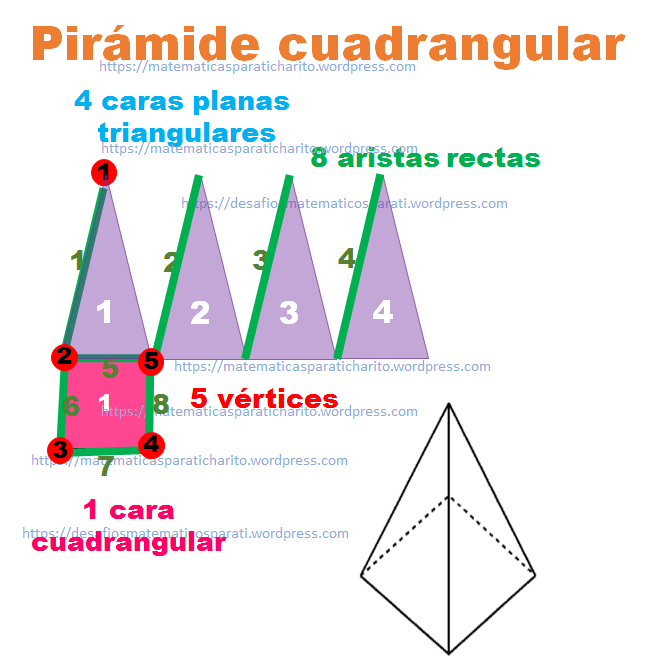
Pirámide cuadrangular. Tiene 5 caras planas, 1 de ellas cuadrangular que es la base; y 4 caras laterales planas triangulares, 5 vértices y 8 aristas rectas.
Cuerpos redondos
Los cuerpos redondos son el cilindro, el cono, la esfera y el toro.
Se caracterizan porque tienen caras curvas y pueden o no tener caras planas.
Veamos sus características.
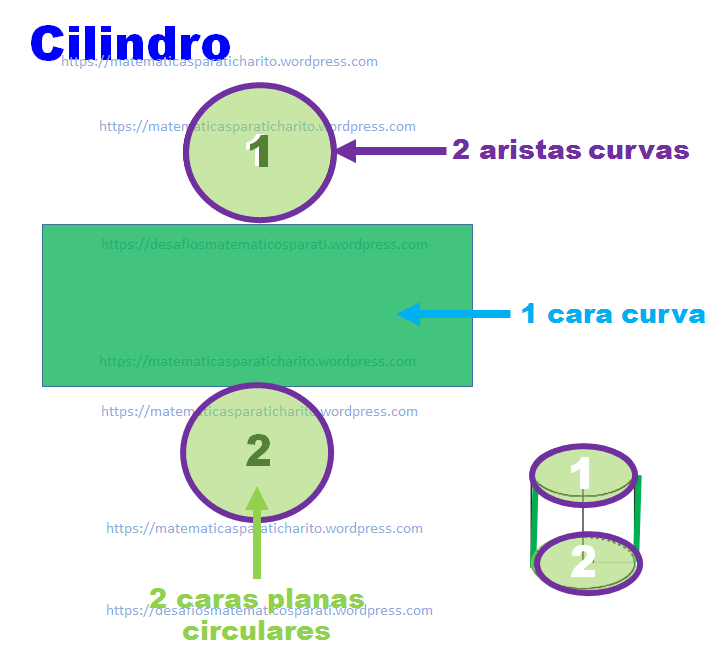

Cilindro. Tiene 2 caras planas circulares que son las bases; y 1 cara lateral curva; 2 aristas curvas, y no tiene vértices.
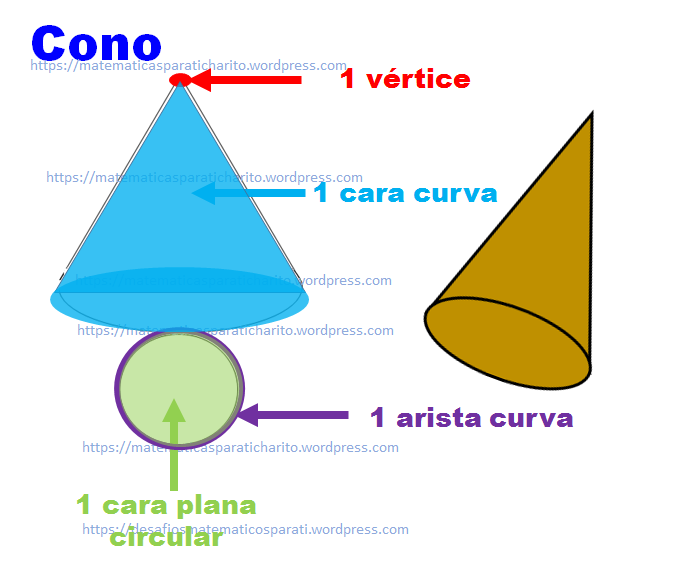
Cono. Tiene 1 cara plana circular que es la base; y 1 cara lateral curva; 1 arista curva, y tiene 1 vértice.
Otros cuerpos redondos son: la esfera, la semiesfera y el toro. No tienen vértices.




















