Giros con el transportador

Pequeños giros

Un ejercicio más de trazo de ángulos.
Abre tu compás con una medida mayor de 6 cm, será la medida del radio de un círculo.

Con esa abertura del compás, traza un círculo en una hoja de papel.

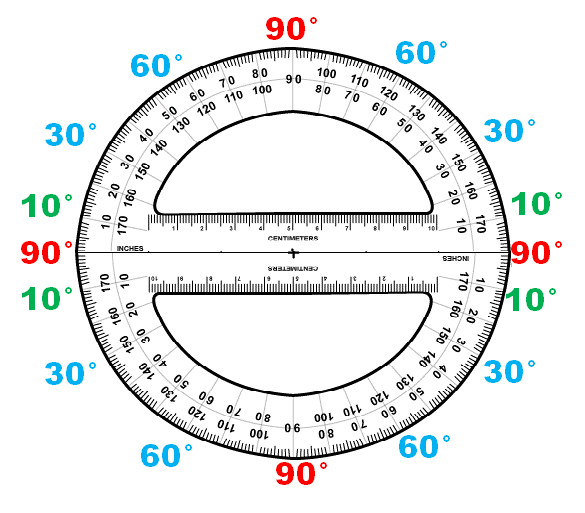
Recorta el círculo y dóblalo en cuatro partes igual (a la mitad, y luego otra vez a la mitad). Repasa las líneas del doblez con color rojo (son cuatro ángulos de 90° y cada uno de ellos representa un cuarto del giro completo). El giro completo corresponde a toda la circunferencia.

Recorta el círculo sobre las cuatro líneas rojas. Te quedarán los cuatro cuartos separados.

Dobla cada cuarto en tres partes iguales y remarca las líneas del doblez con azul (como estás dividiendo 90° en tres partes iguales, cada una de ellas representa un ángulo de 30° y un doceavo del giro completo).

Divide cada tercio del cuarto, en tres partes iguales (te deben de quedar nueve partes iguales en cada cuarto). Marca cada línea del doblez con color verde. Como dividiste 30° en tres partes iguales, cada parte representa un ángulo de 10° y un treinta y seisavo del giro completo.

Si realizas las actividades anteriores en un círculo más pequeño o más grande, las medidas de las fracciones no cambian, ya que la dirección de los lados de las fracciones se mantiene igual (al prolongarlos no cambian de dirección).

Divide en 10 partes iguales, cada una de las nueve partes que hay en un cuarto. Si cada una de esas nueve partes equivale a 10°, al dividirla en 10 partes iguales, cada fracción medirá un grado y tendrás los 90° en un cuarto.

Une nuevamente los cuatro cuartos por las líneas rojas. Date cuenta que en cada cuarto hay 90 °, por lo que al formar otra vez el círculo, tendrás trescientas sesenta partes iguales. Estas 360 partes representan a los 360° en los que se divide la circunferencia.

Si comparas el resultado de este ejercicio con un transportador, podrás darte cuenta que los grados que marcaste corresponden a los grados de las dos escalas que tiene graduadas.

Si quieres saber más acerca de este tema, haz clic en la siguiente liga.
Instrumentos geométricos

Desafío 6. Quinto grado.

Desafío 6. Salón de fiestas

APRENDIZAJE ESPERADO: Reafirmes el aprendizaje adquirido en el desafío anterior y utilices la relación “el dividendo es igual al producto del divisor por el cociente más el residuo, y éste es menor que el divisor” en la resolución de problemas.

Puedes reafirmar tus aprendizajes de este desafío  revisando el tema «La división y la división abreviada» en este sitio. Sólo da clic sobre el tema.
Pon en práctica los aprendizajes del desafío anterior.

En un salón de fiestas se preparan mesas para 12 comensales en cada una.

a) Si asistirán 146 comensales ¿Cuántas mesas deben prepararse?

Planteamiento: Hay 146 comensales y mesas de  12 personas.  ¿Cuántos lugares hay? ¿Son suficientes para las 146 personas?

Resuelve y escribe tu respuesta.

b) ¿Cuántos invitados más podrán llegar como máximo para ocupar los lugares restantes en las mesas preparadas?

Planteamiento: Hay 13 mesas con 12 lugares y hay 146 comensales. ¿Los lugares son exactos, sobran o faltan?

Resuelve y escribe tu respuesta

c) ¿Los invitados podrán organizarse en las mesas de tal manera que queden dos lugares vacíos en cada una? ¿Y podrían organizarse para que quede un lugar vacío?

Planteamiento: Si quedan dos lugares vacíos en cada mesa, entonces caben 10 comensales en cada mesa, si son 146 comensales y 13 mesas, ¿son suficientes los lugares? ¿Por qué?

Si queda un lugar vacío en cada mesa, entonces se sentarán 11 comensales en cada una. Si son 146 comensales y 13 mesas, ¿son suficientes los lugares? ¿Por qué?

d) Una familia de 4 personas quiere sentarse sola en una mesa. ¿Alcanzarán los lugares en las otras mesas para los demás invitados?

Planteamiento: Si son 13 mesas y quito una para la familia de 4 personas, quedan 12 mesas.

Si a las 146 personas le quito las 4 de la familia que se sentará sola, quedan 142 personas.

¿Alcanzan 12 mesas de 12 lugares para las 142 personas? ¿Por qué?

Resuelve y comenta tus respuestas con tus compañeros.

Desafío 4. Quinto grado

Desafío 4. Anticipo el resultado

En este desafío vas a reafirmas los aprendizajes que adquiriste en el desafío 3.
Practica lo aprendido.
Da clic en el siguiente tema para aclarar dudas.
«La división y la división abreviada»

O puedes revisar la información del «Desafío 3. Quinto grado«

Ejercicios resueltos. Cómo construir un cuadrado

Cuadrado

Recuerda que un cuadrado es el polígono regular que tiene sus cuatro lados y sus cuatro ángulos internos iguales A 90°.

Construcción de un cuadrado con instrumentos geométricos

Traza el segmento AB con la medida del lado conocido, en este caso 4 cm.

Levanta la perpendicular del segmento AB en el extremo A

Abre tu compás con la medida del segmento AB y, apoyando con centro en A corta la perpendicular con arco. El punto donde corte, será el tercer vértice de tu cuadro. Ponle la letra D.

Apoyando el centro en D y con la misma abertura del compás, traza un arco desde A hacia arriba.

Ahora, apoyando el centro en B y con la misma abertura del compás, traza otro arco desde A hacia arriba, hasta que corte a los dos arcos trazados anteriormente.

El punto donde se cortan los arcos exteriores es el cuarto vértice del cuadrado. Ponle la letra C.
Une A con C, y E con C para terminar el cuadrado.